Data Structures

Binary Search Tree

Binary Search Tree is a node-based binary tree data structure.

Properties:

• The left subtree of a node contains only nodes with values lesser than the node’s value

• The right subtree of a node contains only nodes with values greater than the node’s value

• The left and right subtrees must each be a Binary Search Tree

• There must be no duplicate nodes

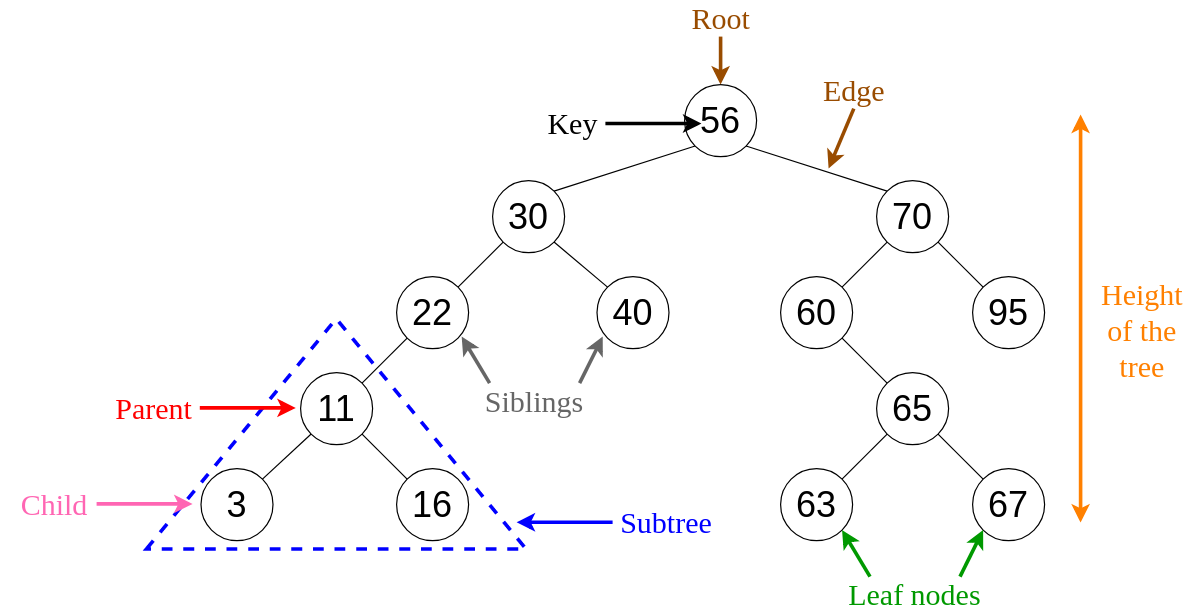
• A Binary Search Tree with height H may have N nodes where

  H ≤ N ≤ 2ᴴ - 1
  

• Inorder traversal of Binary Search Tree always produces sorted output

• We can construct a Binary Search Tree with only Preorder or Postorder or Level Order traversal

• We can always get Inorder traversal by sorting another given traversal

• The longest path’s length of a Binary Search Tree is equal to the Tree’s height

Nodes:

• The top node of a Binary Search Tree is called ‘Root’
• A node with at least 1 ‘Child’ node is called ‘Parent’
• When it has no ‘Children’ nodes, a node is called ‘Leaf’
• ‘Children’ nodes with the same ‘Parent’ can be called ‘Siblings’

A Binary Search Tree can be displayed by a graph (as shown below) or by traversing it.

Traversing the Binary Search Tree

Possible traversals are Preorder, Inorder, Postorder and Level Order.

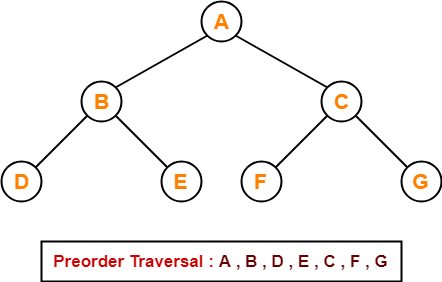
• Preorder

  How it works:

  1. Visit the root
  2. Traverse the left subtree
  3. Traverse the right subtree

  

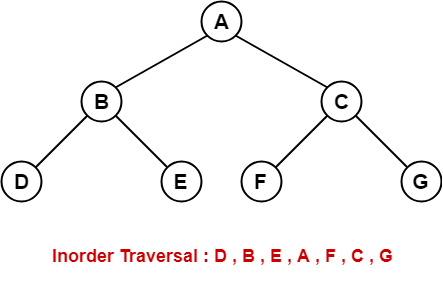
• Inorder

  The Inorder traversal of a Binary Search Tree always returns the nodes in a sorted order.

  How it works:

  1. Traverse the left subtree
  2. Visit the root
  3. Traverse the right subtree

  

• Postorder

  How it works:

  1. Traverse the left subtree
  2. Traverse the right subtree
  3. Visit the root

  

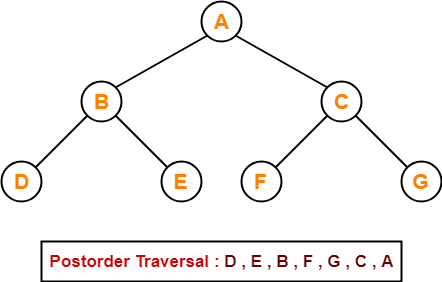
Notice how, in the previous 3 traversals, the root changes priority.

It starts as 1st in Preorder, then 2nd in Inorder and 3rd in Postorder.

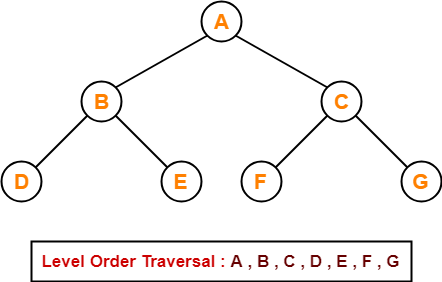
• Level order

  Level order traversal of a tree is Breadth-First traversal for the tree.

  How it works:

  1. Start from level 0 (root)
  2. Print that level
  3. Continue to the lower one
  4. Repeat from step 2

  

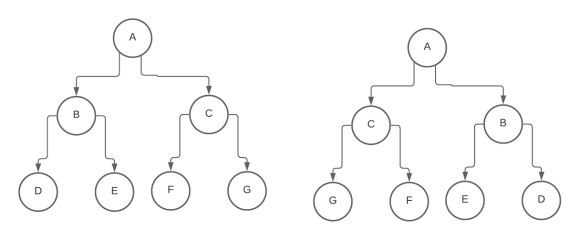
Invert a BST

The goal is simple:

• In a BST, smaller elements go to the left, bigger elements go to the right
• To invert the BST, we place bigger elements to the left and smaller to the right

To achieve this, we simply have to do

for every ‘Parent’ node of the Binary Search Tree.

AVL Tree

An Adelson-Velsky and Landis Tree, or AVL Tree for short, is a self-balancing Binary Search Tree.

Since this is true, it can be traversed in the same way as a BST.

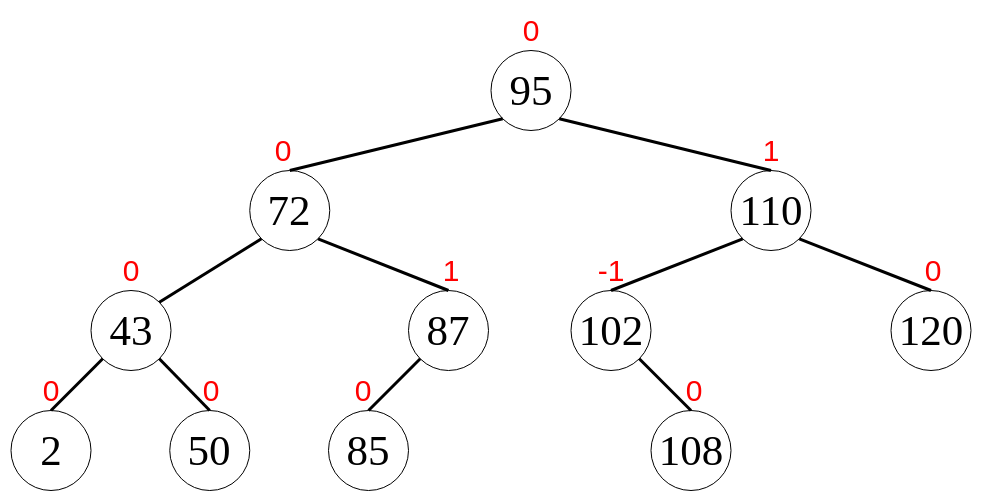
Balance Factor

This is achieved through certain rotations that keep the AVL Tree balanced. Insertions and deletions may require the tree to be rebalanced by one or more rotations.

In general, in a Binary Tree, the Balance Factor of a node X is defined to be the height difference of the 2 child sub-trees.

BF(X) = Height(LeftSubtree(X)) - Height(RightSubtree(X))

If every node X’s Balance Factor is -1, 0, or 1 (BF(X)∈{-1,0,1},∀ X) then our tree is defined as AVL Tree.

A node X with

• BF(X) < 0 is called “left-heavy”
• BF(X) > 0 is called “right-heavy”
• BF(X) = 0 is called “balanced”

Rebalancing

During insert and delete operations a (temporary) height difference of 2 may arise, which means that the parent sub-tree has to be “rebalanced”.

Let X be the node that has a (temporary) balance factor of −2 or +2. Its left or right subtree was modified. Let Z be the child with the biggest height.

There are four possible variants of the violation:

• Right Right => Z is a right child of its parent X and BF(Z) ≥ 0
• Left Left => Z is a left child of its parent X and BF(Z) ≤ 0
• Right Left => Z is a right child of its parent X and BF(Z) < 0
• Left Right => Z is a left child of its parent X and BF(Z) > 0

The rebalancing is performed differently:

• Right Right => X is rebalanced with a simple rotation rotate_Left
• Left Left => X is rebalanced with a simple rotation rotate_Right
• Right Left => X is rebalanced with a double rotation rotate_RightLeft
• Left Right => X is rebalanced with a double rotation rotate_LeftRight

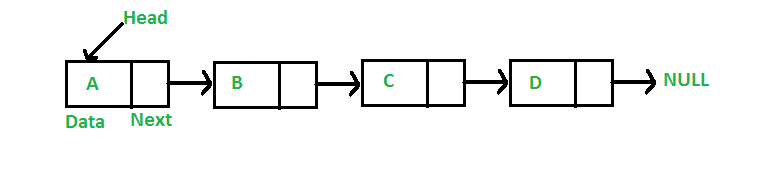
Singly Linked List

Singly Linked List is basically a one-way chain of nodes.

The list has a ‘Head’ node that serves as its first of the chain.

Each node has a value and a pointer “pointing” to the next node.

Doubly Linked List

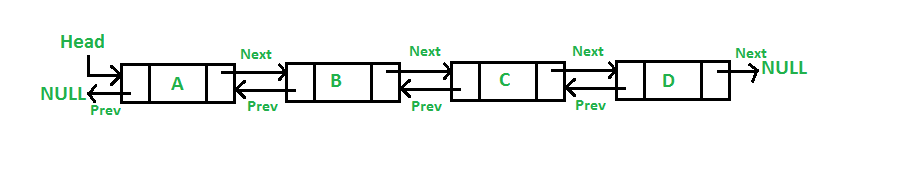
Doubly Linked List is similar to the Singly Linked List with a few additions.

Each node has an extra pointer that “points” to the previous node too.

The list itself, instead of a reference to the ‘Head’ node, also has one for the ‘Tail’ node of the list, the last.

This type of Linked List can be traversed either starting from the ‘Head’ or the ‘Tail’ node.

Circular Linked List

Circular Linked List is similar to the Singly Linked List with 1 basic change.

The last node of this Linked List always points to the ‘Head’ creating an endless chain.

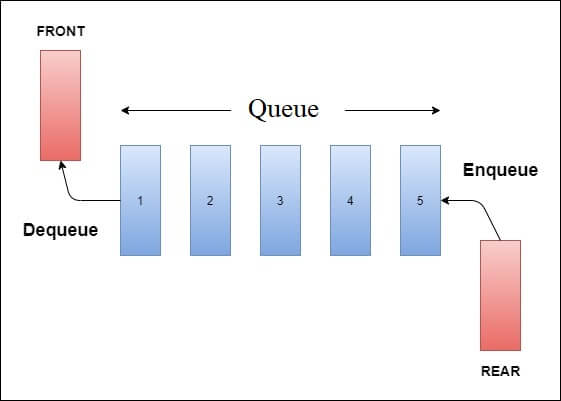
Queue

Queue is a linear structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO).

A good example of queue is any queue of consumers for a resource where the consumer that came first is served first.

Operations:

• Front

  Get the front element of the queue

• Rear

  Get the rear element of the queue

• Enqueue

  Add an element to the rear of the queue

• Dequeue

  Remove the front element of the queue

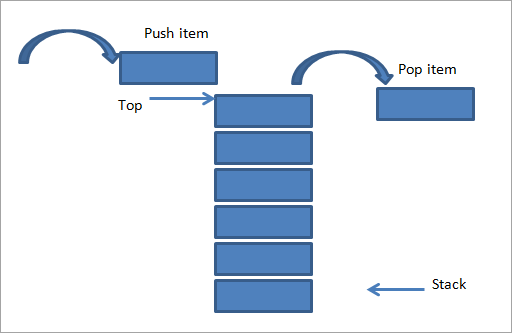
Stack

Stack is a linear structure which follows a particular order in which the operations are performed. The order is Last In First Out (LIFO).

A good example of stack can be a stack of plates in a canteen. The last plate to go to the stack is the first one to get removed, to either be used or washed.

Operations:

• Push

  Adds an item in the stack

• Pop

  Removes an item from the stack

• Top

  Returns top element of stack

• isEmpty

  Returns true if stack is empty, else false

Resources

• GeeksForGeeks
• my GitHub repository