Algorithms
Search Algorithms
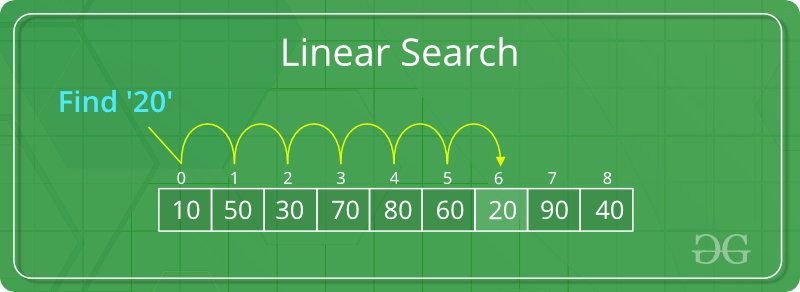
Linear Search
Time Complexity: O(n)
As the name implies, it works in a linear manner.
Start from the left-most element of the array and one by one compare each with x.
Binary Search
Time Complexity: O(log n)
Binary Search is another basic search algorithm. Unlike Linear Search, it needs a sorted array of elements to work.
Basically, using the 2 edges of the array, we compare the middle element with x.
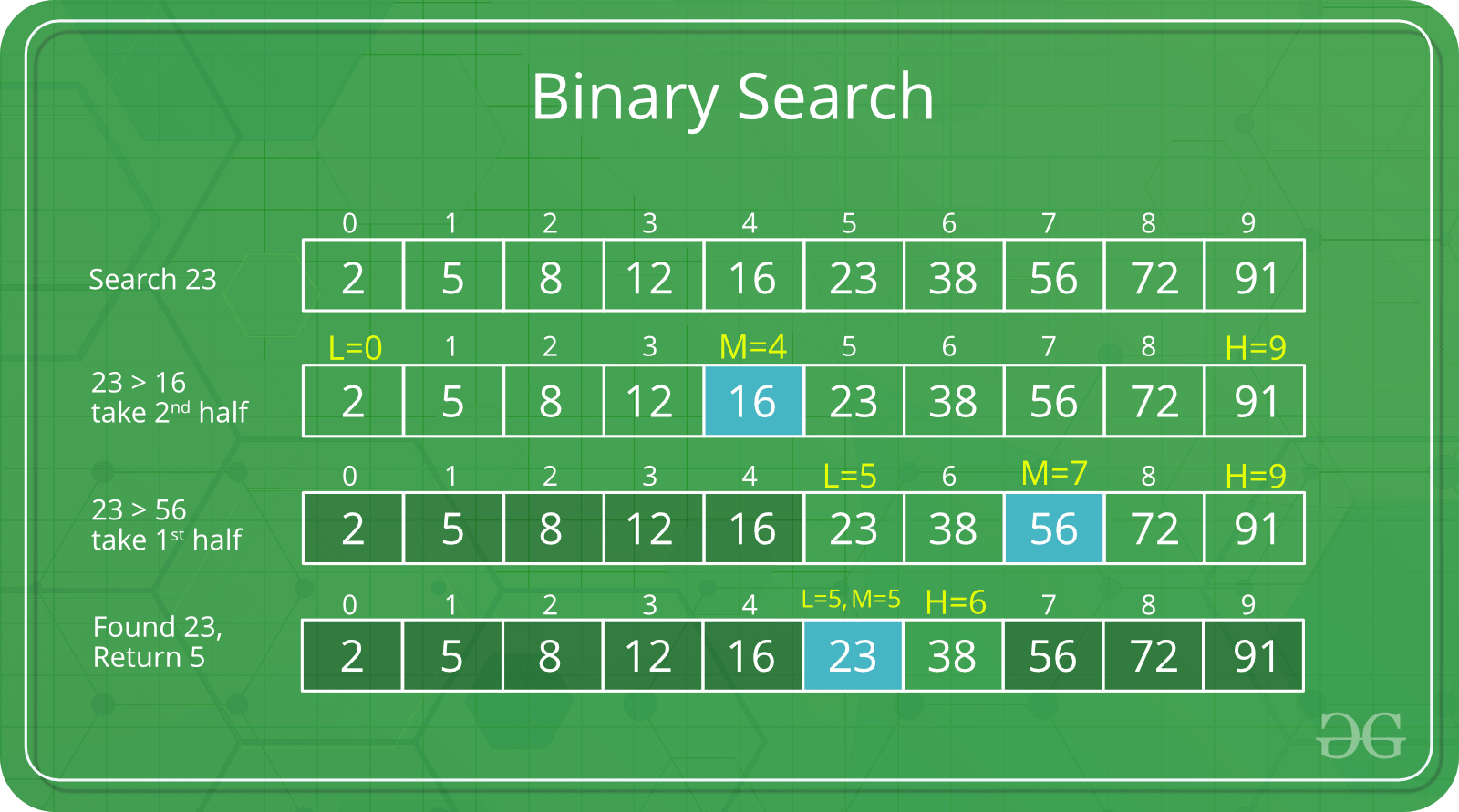
Notice that after each comparison, we ignore half of the elements we had.
Exponential Search
Time Complexity: O(log n)
First, we search for the range where element is present.
This is achieved by starting with subarray size 1, compare its last element with x, then doubling the size until last element of a subarray is not greater.
Once we find an index i, we just have to search in the range [i/2, i]. To do so, we use Binary Search.
Like Binary Search, we need a sorted array to work with.
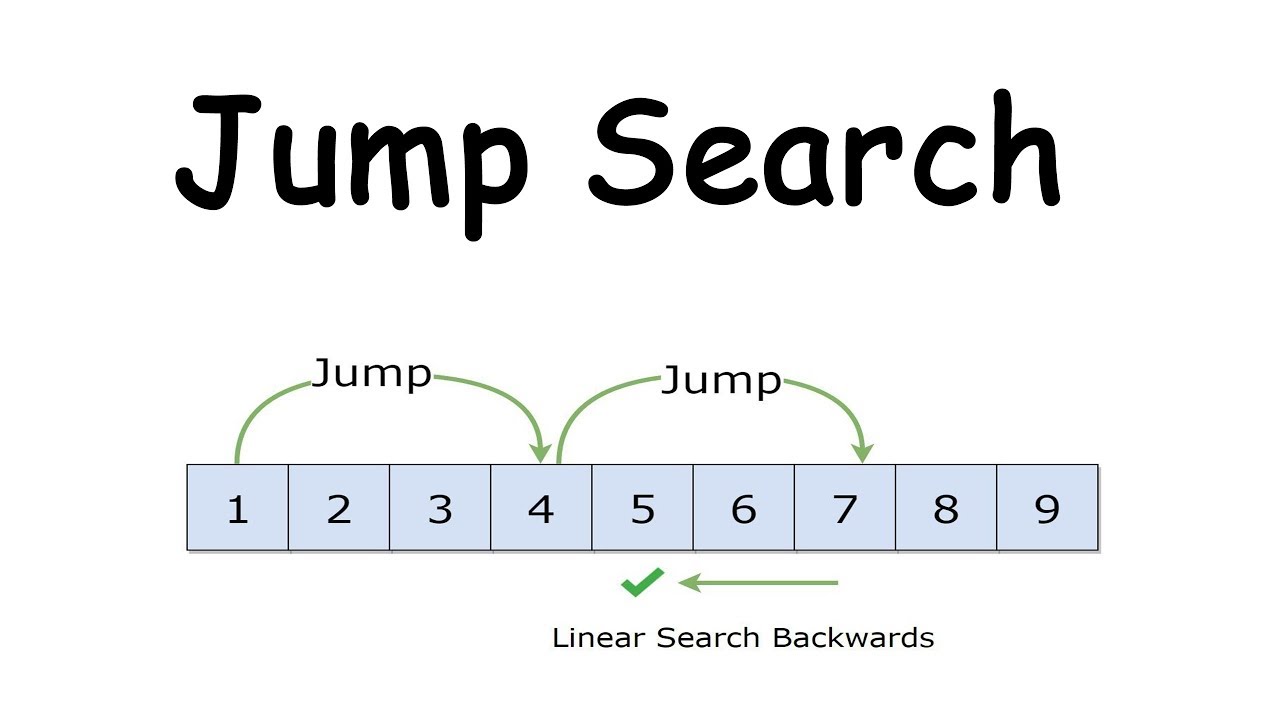
Jump Search
Time Complexity: O(√n)
Like Binary Search, Jump Search is a searching algorithm for sorted arrays.
The basic idea is to check fewer elements (than Linear Search) by jumping ahead by fixed steps or skipping some elements in place of searching all elements.
Then, we Linear Search backwards from there until we find the element or we reach the index of the previous step. (i-step)
After each jump, we compare the current element with x.
Sort Algorithms
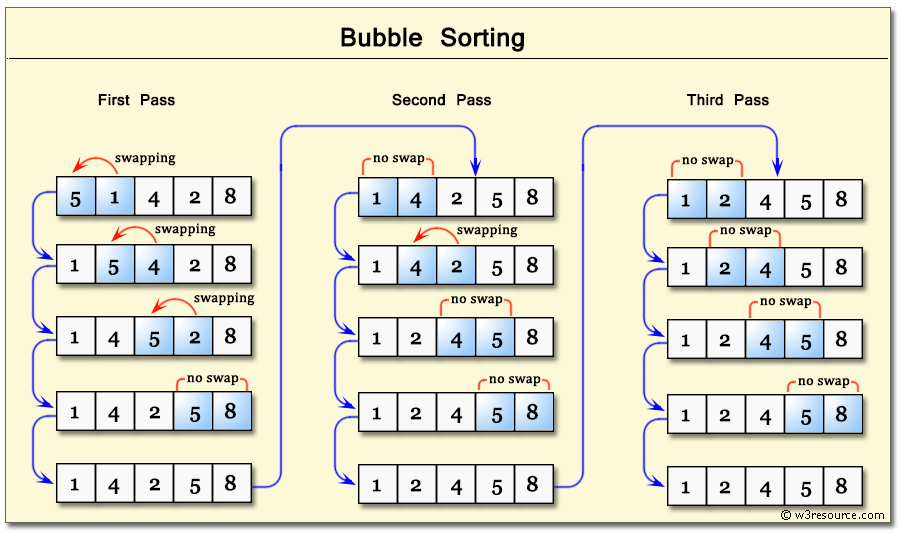
Bubble Sort
Time Complexity: O(n)
Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.
Counting Sort
Time Complexity: O(n+k) where n is the number of elements in input array and k is the range of input.
Counting Sort is similar to hasing. It works by counting the number of objects having distinct key values.
For examle, take the array
[1, 4, 1, 2, 7, 5, 2]
So, we make an array to count our elements
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| count | 0 | 2 | 2 | 0 | 1 | 1 | 0 | 1 |
or
[0, 2, 2, 0, 1, 0, 1]
as we have x0 0s, x2 1s and so on.
The result would be
[1, 1, 2, 2, 4, 5, 7]
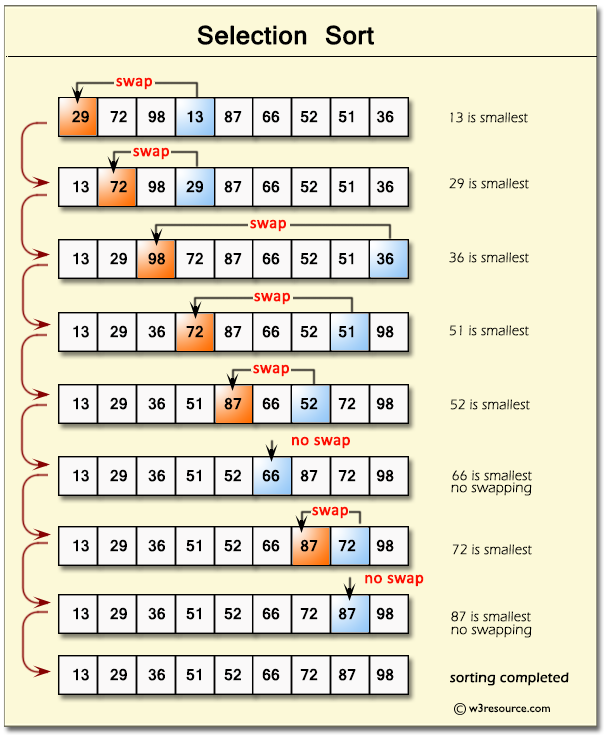
Selection Sort
Time Complexity: O(n²)
Basically, we devide the array into 2 subarrays, 1 sorted and 1 unsorted.
Start from the left-most element and with each iteration, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.